ฟังก์ชันเวียนเกิด

ฟังก์ชันเวียนเกิด (Recursive Function) คือฟังก์ชันที่มีการคืนค่าเป็นตัวฟังก์ชันนั้นเอง ทำให้ต้องมีการเรียกใช้ตัวฟังก์ชันนั้นซ้ำ และในฟังก์ชันที่เรียกซ้ำนั้น ก็มีการเรียกฟังก์ชันเดิมซ้ำอีก วนเวียนอย่างนี้ไปเรื่อยๆ จนถึงจุดหนึ่ง จะมีเงื่อนไขที่ทำให้ฟังก์ชันนั้นคืน ค่ากลับโดยที่ไม่ต้องเรียกฟังก์ชันซ้ำอีก การวนซ้ำจึงหยุดลง อธิบายด้วยคำพูดแบบนี้ยังไงก็คงจะยังเข้าใจยากอยู่ มาดูตัวอย่างน่าจะช่วยให้เห็นภาพชัดกว่า

แฟ็กทอเรียล

ฟังก์ชันแฟ็กทอเรียลนั้นเป็นหนึ่งในตัวอย่างที่ง่ายที่สุดของการใช้ฟังก์ชันเวียนเกิด
ลองดูตัวอย่างการใช้ สร้างฟังก์ชัน fac(x) = x! = 1×2×3×...×x

def  fac(x):  
if(x>1):  
return  fac(x-1)*x  
else:  
return  1  
  
print(fac(6))  # ได้ 720

จะเห็นว่าฟังก์ชัน fac ในที่นี้มีการเรียกตัวมันเองคือฟังก์ชัน fac ซ้ำอีกภายในนั้น การเรียกซ้ำนี้จะเกิดขึ้นตราบใดที่ยังมากกว่า 1 แต่ถ้าเป็น 1 จะคืนค่า 1 โดยไม่มีการเรียกซ้ำ ลองนึกตามทีละขั้น สมมุติเราเรียกใช้ฟังก์ชันโดยใส่อาร์กิวเมนต์เป็น 1 คือ fac(1)
แบบนี้ฟังก์ชันจะเข้า else ทันทีเพราะ x เป็น 1 ดังนั้นจึงคืนค่า 1 กลับมา ซึ่งเป็นไปตามที่ควรจะเป็น

ต่อไปลองคิดกรณี fac(2) กรณี นี้เมื่อเรียกใช้ x=2 จะเข้าเงื่อนไขแรก ซึ่งจะต้อง return fac(x-1)*x ทำให้มีการเรียกใช้ฟังก์ชันนั้นซ้ำ แต่คราวนี้อาร์กิวเมนต์ต่างไปโดยลดลงไป 1 เป็น x-1 ก็คือเหลือ 1 ซึ่งจะคืนค่า 1 กลับมา จากนั้นก็ถูกนำไปคูณกับ x ก็คือ 2 ดังนั้นผลที่ได้ก็คือได้ 2

คิดต่อไป กรณี fac(3)

เมื่อ เรียกใช้ x=3 จะเข้าเงื่อนไขแรก เรียก return fac(x-1)*x เมื่อแทนค่า x จะได้เป็น return fac(2)*3 ซึ่ง fac(2) ก็รู้ค่าแล้วจากกรณี x=2 ว่าเป็น 2 ดังนั้นเอามาคูณกันก็ได้ผลลัพธ์เป็น 6

กรณี x=4 ก็จะ return fac(3)*4 จึงได้ผลเป็น 24
กรณี x=5 ก็จะ return fac(4)*3 จึงได้ผลเป็น 120
กรณี x=6 ก็จะ return fac(5)*4 จึงได้ผลเป็น 720

เป็นอย่างนี้ซ้ำไปเรื่อยๆเป็นจำนวนครั้งตามค่าของ x ที่ใส่ลงไป เพราะเมื่อเรียกใช้ฟังก์ชัน ภายในฟังก์ชันจะมีการเรียกฟังก์ชันเดิมซ้ำด้วย x ที่ต่ำลงไปทีละขั้น พอเรียกซ้ำก็จะเรียก x ที่ต่ำลงไปเรื่อยๆจนในที่สุดก็เป็น 1 และไม่มีการเรียกซ้ำอีก

สุดท้ายผลที่ได้จึงเป็นการคูณสะสมเพิ่มไปเรื่อยๆ กลายเป็นฟังก์ชันแฟ็กทอเรียลตามที่ต้องการ หากจะลองเขียนเป็นฟังก์ชันธรรมดาที่ไม่ต้องมีการเวียนเกิดก็สามารถทำได้โดยใช้การวนทำซ้ำ ลองเปรียบเทียบกันดู

def  fac(x):  
f = 1  # ตั้งต้นที่ 1  
for  i  in  range(2,x+1):  # ใช้ for วนซ้ำ ไล่ตั้งแต่ 2  
f = f*i  # คูณเพิ่มไปเรื่อยๆ  
return  f  # คืนผลลัพธ์ที่ได้กลับไป  
  
print(fac(6))

ข้อดีข้อเสียของการใช้ฟังก์ชันแบบเวียนเกิดเมื่อเทียบกับการไม่ใช้

ข้อดี

• หากใช้ได้คล่องแล้วจะมองปัญหาออกได้ง่ายขึ้น เข้าใจง่ายกว่า
• เขียนแล้วดูสั้นกว่า
• ง่ายกว่ามากในกรณีที่มีการทำซ้ำซ้อนกันเป็นวังวนในจำนวนที่ไม่แน่นอน

ข้อเสีย

• เปลืองหน่วยความจำมากกว่า
• ในบางกรณีอาจทำงานช้ากว่า

สรุปก็คือวิธีการนี้ไม่ได้ทำให้โปรแกรมทำงานเร็วขึ้น แถมอาจช้าลงอีก เพียงแต่ในบางปัญหาจะทำให้ดูเรียบง่ายขึ้น เขียนฟังก์ชันสั้นเกินคาดทั้งๆที่น่าจะซับซ้อน ดังนั้นที่สำคัญคือมองปัญหาให้ออกว่าเวลาไหนควรจะใช้ เลือกใช้ตามความเหมาะสม เพื่อให้เห็นภาพชัดลองดูตัวอย่างอื่นเปรียบเทียบกันอีก

ฟีโบนัชชี

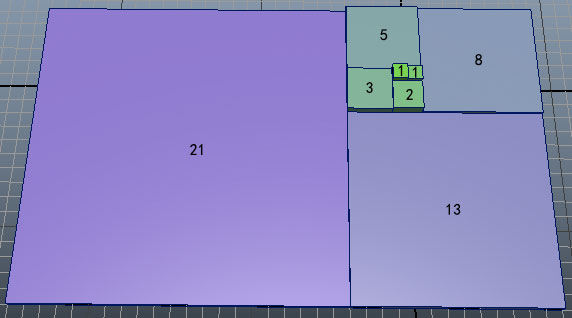
ลำดับฟีโบนัชชี (Fibonacci) คือลำดับที่มีสมาชิก ๒ ตัวแรกมีค่าเท่ากับ 1 นอกนั้นตัวถัดไปจะมีค่าเท่ากับสองตัวก่อนหน้าบวกกัน
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ... ลองมาเขียนเป็นฟังก์ชันในไพธอนดู

def  fib(x):  
if(x>2):  
return  fib(x-1)+fib(x-2)  
else:  
return  1  
  
print(fib(8))

จะเห็นว่าฟังก์ชันนี้มีการกำหนดเงื่อนไขตามที่ได้กล่าวข้างต้น คือถ้า x เป็นตัวที่ 1 หรือ 2 จะมีค่าเป็น 1 แต่ถ้าเป็นตัวถัดจากนั้นจะมีค่าเท่ากับสองตัวก่อนหน้าบวกกัน ฟังก์ชันแบบนี้ถ้าไม่ใช้เป็นแบบเวียนเกิด ใช้การวนซ้ำธรรมดาจะเป็นอย่างไร

def  fib(x):  
a = 1  
b = 1  
f = 1  
for  i  in  range(3,x+1):  
f = a+b  
a = b  
b = f  
return  f  
  
print(fib(8))

คราวนี้จะเห็นว่าใช้ฟังก์ชันแบบเวียนเกิดดูแล้วการเขียนดูเรียบง่ายกว่าพอสมควร แต่อย่างไรก็ตาม ภายใต้ความเรียบง่ายของมัน ก็แฝงไปด้วยความน่ากลัว ลองพิจารณาดูจะเห็นว่ากรณีใช้ฟังก์ชันเวียนเกิดนั้นเมื่อเรียกใช้ฟังก์ชันครั้ง หนึ่งจะมีการเรียกตัวมันเองถึง ๒ ครั้ง คือ fib(x) จะมีการเรียก fib(x-1) และ fib(x-2) ขึ้นมา และภายในนั้น fib(x-1) ก็จะทำการเรียก fib(x-2) และ fib(x-3) ส่วน fib(x-2) ก็ไปเรียก fib(x-3) กับ fib(x-4) แล้วก็วนเรียกซ้ำเพิ่มไปเรื่อยๆ จำนวนครั้งที่เรียกมีแต่จะเพิ่มขึ้นเรื่อยๆเป็นทวีคูณ

การเรียกในแต่ละครั้งเป็นการคำนวณใหม่ทุกครั้ง แม้ว่า fib(x-2) จะถูกเรียกซ้ำ 2 ครั้ง fib(x-3) ถูกเรียกซ้ำ 3 ครั้ง แต่มันก็ไม่ได้เก็บค่าเดิมเอาไว้ แต่กลับคำนวณใหม่แยกกัน ผลก็คือเครื่องทำงานหนักและประสิทธิภาพการทำงานต่ำ ในขณะที่ถ้าใช้ for วนซ้ำธรรมดา ตัวแปรมีการเก็บค่าเสร็จแล้วก็นำมาใช้แล้วล้างใหม่ทุกรอบ พอเป็นแบบนี้แล้วเครื่องจึงทำงานเบากว่ามาก

สรุป กรณีนี้ฟังก์ชันเวียนเกิดเขียนง่ายแต่ประสิทธิภาพแย่ ฟิโบนัชชีจึงเป็นตัวอย่างของกรณีที่ไม่ควรจะใช้ บางครั้งการเขียนสั้นไม่ได้แปลว่าเป็นโปรแกรมที่ดี ต้องพิจารณาด้วยว่าโปรแกรมมีการทำงานอย่างไรอยู่เบื้องหลังคำสั่งนั้น

ฟังก์ชันสำหรับยุบลิสต์

ลองดูตัวอย่างการใช้ที่ไม่ได้เกี่ยวข้องกับฟังก์ชันทางคณิตศาสตร์กันบ้าง ตัวอย่างหนึ่งที่จะช่วยให้เห็นว่าใช้ฟังก์ชันเวียนเกิดแล้วง่ายก็คือการยุบลิสต์ สมมุติว่ามีลิสต์หน้าตาซับซ้อนแบบนี้อยู่ [[['a','b'],['c','d']],[['e','f'],['g',['h','i']]],['j','k'],'l']

จะเห็นว่าเป็นลิสต์ซ้อนกันหลายชั้น สูงสุดคือ h กับ i นี้ซ้อนอยู่ในชั้นที่ ๔ คือเป็นลิสต์ในลิสต์ในลิสต์ในลิสต์ เราจะทำให้ทั้งหมดนี้มาอยู่ในลิสต์อันเดียว คือกลายเป็น ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l'] สามารถทำได้ด้วยการสร้างฟังก์ชันเวียนเกิด

def  yup(l):  
y = []  # สร้างลิสต์เปล่าขึ้นมาก่อน  
for  c  in  l:  
if(type(c)==list):  # ตรวจชนิดของสมาชิกว่าเป็นลิสต์หรือเปล่า  
y += yup(c)  # ถ้าเป็นลิสต์ให้เรียกฟังก์ชันซ้ำเพื่อยุบก่อนค่อยเพิ่มเข้าไป  
else:  
y += [c]  # ถ้าไม่ใช่ลิสต์ให้เพิ่มเข้าไปในสมาชิก  
return  y  # คืนค่าลิสต์ที่ได้  
  
lia = [[['a','b'],['c','d']],[['e','f'],['g',['h','i']]],['j','k'],'l']  
print(yup(lia))

ในนี้จะเห็นว่าฟังก์ชัน yup มีการเรียกใช้ตัวมันเองในกรณีที่สมาชิกเป็นลิสต์ เพื่อให้ลิสต์นั้นยุบก่อนที่จะบวกเพิ่มเข้าไป ถ้าภายในลิสต์นั้น มีลิสต์อยู่อีกจึงทำการเรียกตัวเองซ้ำอีก ปัญหานี้ยากที่จะใช้การวนซ้ำด้วย for เพราะเราไม่รู้ว่าจะต้องมีวังวนซ้อนอยู่กี่ชั้น

หอคอยฮานอย

ตัวอย่างปัญหาอีกอย่างที่ดูเหมือนจะยากแต่ถ้าใช้ฟังก์ชันเวียนเกิดจะดูแล้วง่ายลงไปทันที

รายละเอียดเขียนไว้ใน https://phyblas.hinaboshi.com/20160301

อ้างอิง

http://www2.cc.niigata-u.ac.jp/~takeuchi/tbasic/BackGround/Recursive.html

Reference : https://phyblas.hinaboshi.com/tsuchinoko20